Métodos de subespacios de Krylov
y sus aplicaciones a la Dinámica Browniana
Edwin Armando Bedolla Montiel
12 de febrero, 2021, Grupo de Materia Blanda.
Contenido
- ¿Qué son los métodos de subespacios de Krylov?
- ¿En qué problemas se pueden emplearse?
- ¿Cómo se implementan?
- Ejemplos: sistemas lineales y regresión lineal.
- Interacciones hidrodinámicas en dinámica Browniana.
Definición
Sea \( A \) una matriz invertible de \( n \times n \), y sea \( b \) un vector de dimensión \( n \), entonces, un subespacio de Krylov de orden \( r \) está definido como \[\begin{equation} \mathcal{K}_r(A, b) = \text{span} \{ b, Ab, A^2 b, A^3 b, \dots, A^{r-1} b\} \end{equation} \]Aproximaciones
Esto significa que podemos crear un subespacio lineal usando solamente el producto \( Ab. \)Regresión lineal
Se quiere resolver el problema \[ \mathbf{y}=\mathbf{X \beta} + \alpha + \mathbf{\epsilon} \] donde \( \beta \) es el vector de coeficientes y \( \alpha \) es conocido como el sesgo u ordenada al origen.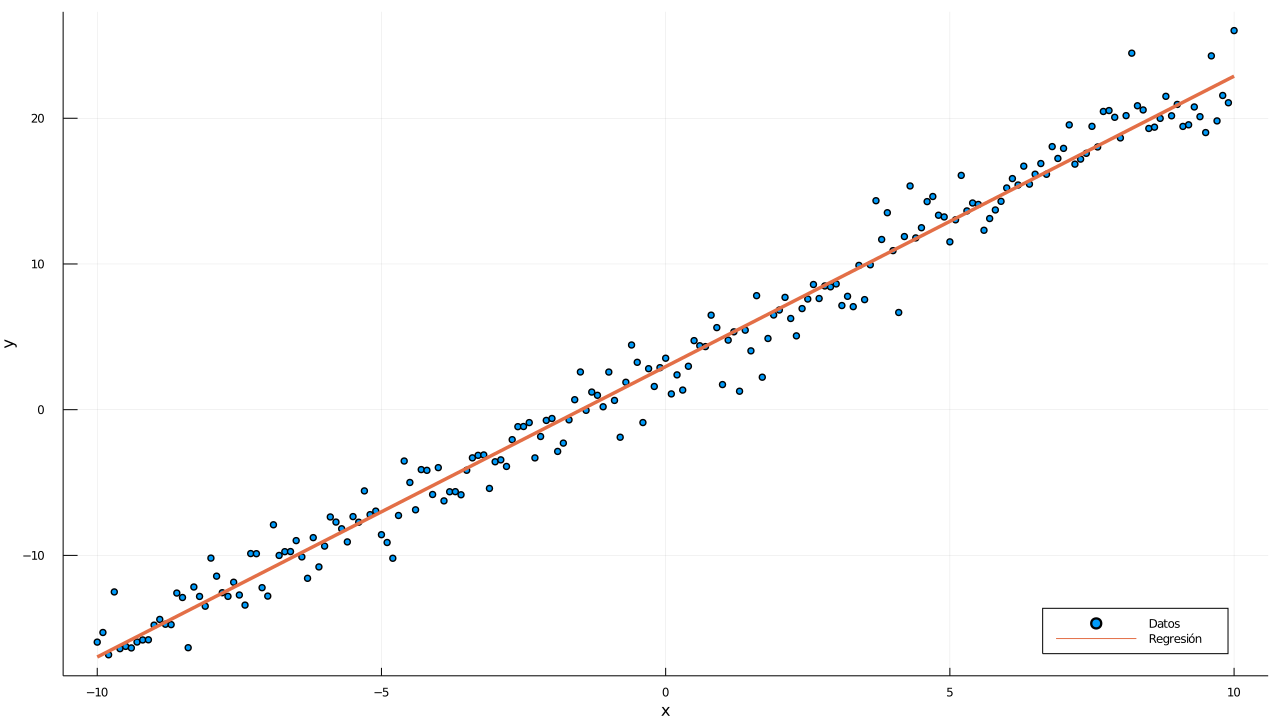
Método del gradiente conjugado
Implementación
Este algoritmo es rápido, y tiene la gran ventaja de que es fácil de implementar.Definiciones y asignaciones
Sea \( A=\mathbf{X^{\mathsf{T}} X} \) y \( \mathbf{b} = \mathbf{X^{\mathsf{T}} y} \), entonces \[ \begin{align} & x_0 := \mathbf{0} \text{ solución inicial} \\ & \mathbf{r}_0 := \mathbf{b} - \mathbf{A x}_0 \\ & \mathbf{p}_0 := \mathbf{r}_0 \\ & k := 0 \\ \end{align} \] Aquí, \( \mathbf{p} \) es la notación para los vectores base que formarán el espacio lineal de los residuos, \( \mathcal{K}_{residuos} \).\( \alpha_k \) son los coeficientes de la combinación lineal en \( \mathcal{K}_{residuos} \).
\( \beta_k \) son los coeficientes de la combinación lineal en \( \mathcal{K}_r \).
Condiciones
El método del gradiente conjugado solamente funciona si la matriz \( A \) es simétrica y definida positiva.
Si no lo es, otro método debe emplearse.
Alternativas
- GMRES (Generalized minimal residual method)
- BiCG (Biconjugate gradient method)
- BiCGSTAB (Biconjugate gradient stabilized method)
Dinámica Browniana
En el 2012, Ando et al. propusieron emplear métodos de subespacios de Krylov.
Se dieron cuenta que el problema es calcular \( \mathbf{D^{1/2}} ,\) esto porque \(\mathbf{D}=\mathbf{D^{1/2}} \mathbf{(D^{1/2})}^{\mathsf{T}} \)
Además, se dieron cuenta que no necesitan saber \( \mathbf{D^{1/2}} \) sino \( \mathbf{D^{1/2} z} .\)
Después de todo, solamente son desplazamientos estocásticos, no deben ser precisos, sino aproximados.
Propuesta
Construir un subespacio de Krylov para realizar esta aproximación, tal que \[ \mathcal{K}_m(\mathbf{D, z})=\text{span } \{ \mathbf{z}, \mathbf{Dz}, \mathbf{D^{1/2}z}, \dots, \mathbf{D^{m-1}z} \} \]Asignaciones
\[ \mathbf{z} \sim \mathcal{N}(0, \mathbf{I}) \\ j := 0 \text{ contador de bucle} \\ \qquad v_0 := \frac{\mathbf{z}}{\lVert \mathbf{z} \rVert} \\ m := 30 \text{ el tamaño del subespacio de Krylov} \\ \]Se hizo una aproximación de la matriz \( D^{1/2} \); esta aproximación es la matriz \( H^{1/2} .\)
Se va ortognalizando el espacio según se necesiten vectores.
Pasamos de un espacio de \( 3n \times 3n \) a un espacio \( m \times m \) donde \( m \ll 3n \), en este caso, \( m \equiv 30 .\)
znorm = dnrm2( s,xr,1 )
vm(:,1) = xr / znorm
do i = 1,m
call dgemv( 'n',s,s,1.0_dp,sigma,s,vm(:,i),1,0.0_dp,w,1 )
if ( i > 1 ) then
w = w - ( h(i-1,i) * vm(:,i-1) )
end if
k = size(w, 1)
h(i,i) = ddot( k,w,1,vm(:,i),1 )
if ( i < m ) then
w = w - ( h(i,i) * vm(:,i) )
k = size(w, 1)
h(i+1,i) = dnrm2( k,w,1 )
h(i,i+1) = h(i+1,i)
vm(:,i+1) = w / h(i+1,i)
end if
end do
call sqrt_matrix( h,temp )
call dgemv( 'N',m,m,1.0_dp,temp,m,eid,1,0.0_dp,v,1 )
call dgemv( 'N',s,m,1.0_dp,vm,s,v,1,0.0_dp,res,1 )
r = znorm * res
¿Dónde encontrar estas implementaciones?
Fortran
Python
- Scipy , contiene una colección de estos métodos, algunos son envolturas (e.g. ARPACK), pero ya no es necesario implementarlos.
Julia
- IterativeSolvers , es un paquete con una colección de rutinas para sistemas lineales.
- Krylov , acepta no solamente matrices, sino cualquier tipo de operador lineal.
Conclusiones
-
Los métodos de subespacios de Krylov son métodos iterativos para encontrar resultados aproximados.
-
Dependiendo de las propiedades de las matrices (u operadores lineales), se deben emplear variaciones de estos métodos.
-
Se estudió un caso particular aplicado a la dinámica Browniana.
Referencias
- Strang, G. (1993). Introduction to linear algebra (Vol. 3). Wellesley, MA: Wellesley-Cambridge Press.
- Demmel, J. W. (1997). Applied numerical linear algebra. Society for Industrial and Applied Mathematics.
- Van der Vorst, H. A. (2003). Iterative Krylov methods for large linear systems (No. 13). Cambridge University Press.
- Hestenes, M. R., & Stiefel, E. (1952). Methods of conjugate gradients for solving linear systems (Vol. 49, No. 1). Washington, DC: NBS.
Referencias
- Cipra, B. A. (2000). The best of the 20th century: Editors name top 10 algorithms. SIAM news, 33(4), 1-2.
- Gutknecht, M. H. (2007). A brief introduction to Krylov space methods for solving linear systems. In Frontiers of Computational Science (pp. 53-62). Springer, Berlin, Heidelberg.
- Ermak, D. L., & McCammon, J. A. (1978). Brownian dynamics with hydrodynamic interactions. The Journal of chemical physics, 69(4), 1352-1360.
Referencias
- Ando, T., Chow, E., Saad, Y., & Skolnick, J. (2012). Krylov subspace methods for computing hydrodynamic interactions in Brownian dynamics simulations. The Journal of chemical physics, 137(6), 064106.
- Shewchuk, J. (1994). An Introduction to the Conjugate Gradient Method Without the Agonizing Pain.
- Yamakawa, H. (1970). Transport Properties of Polymer Chains in Dilute Solution: Hydrodynamic Interaction. The Journal of Chemical Physics, 53(1), 436–443. https://doi.org/10.1063/1.1673799
Proyectos
- dbfort Dinámica Browniana en Fortran 2008+.
- LeastSquaresSVM Machine Learning con Máquinas de Soporte Vectorial.